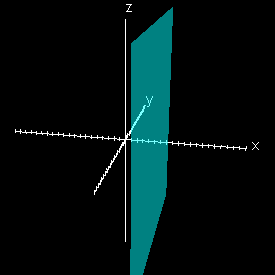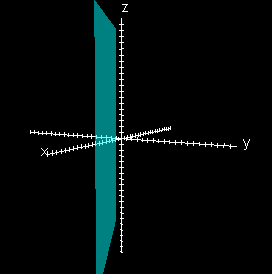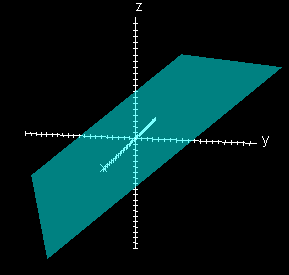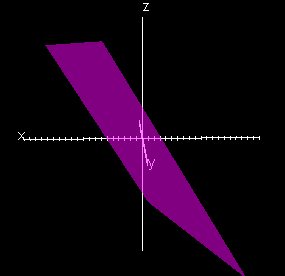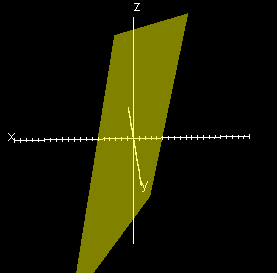Set 1

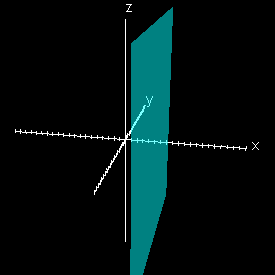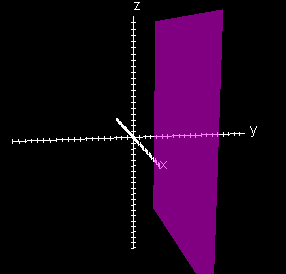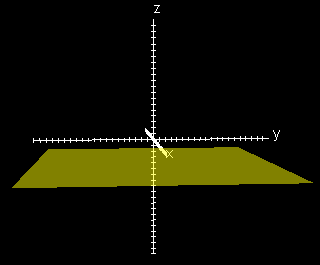
x = 5	y = 8	z = -4
Each of these graphs is parallel to a plane. For example the graph of x = 5 is parallel to the y-z plane with x intercept of 5. How would the other two be described? the graph of y = 8 is parallel to the x-z plane with y intercept of 8 the graph of z = -4 is parallel to the x-y plane with z intercept of -4

Set 2

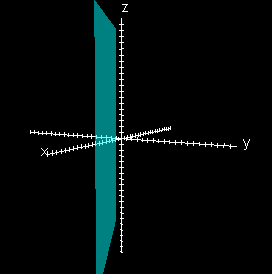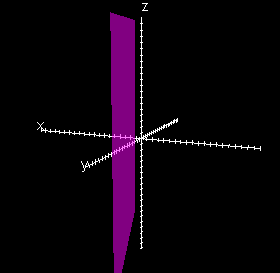
x – 2y = 5	3x + y = 8	5x + z = -4
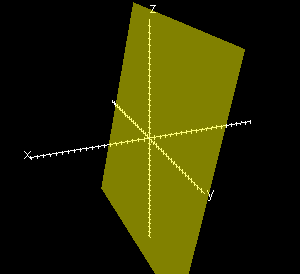Each of these graphs is parallel to an axis. For example the graph of x – 2y = 5 is parallel to the z axis. How would the other two be described? the graph of 3x + y = 8 is parallel to the z axis the graph of 5x + z = -4 is parallel to the y axis

Set 3

x -2y +3z = 5	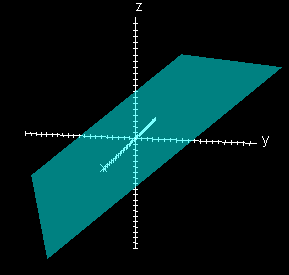3x + y – 2z = 8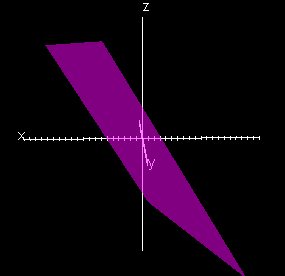	5x – 2y + z = -4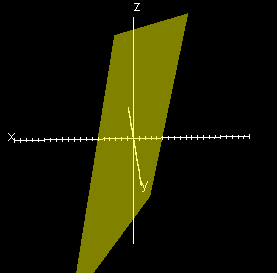
Each of these graphs is not parallel to a plane or axis.

The differences between the graphs of each set are that for set 1 (equations in the form Ax = D, By = D or Cz = D) all of the graphs are parallel to specific planes. For set 2 (equations in the form Ax + By = D, Ax + Cz = D or By + Cz = D) all of the graphs are parallel to specific axes. And for set 3 (equations in the form Ax + By Cz = D) all of the graphs are not parallel to any planes or axes.